最も遠くに投げるには?どの角度に投げると良いのでしょうか。答えは45度です。
真横に投げたら0度、真上に投げたら90度。その間、ちょうど斜めの方向、45度向かって投げると飛距離が最大になるのです。
横に投げると直ぐに重力で下に落ちてしまい、上に投げると前に進まないので、斜めに投げるのが良いのです。斜めに投げることが一番遠くに飛ばす良い方法であることは皆んな知っています。しかし、30度がいいのか、45度がいいのか、60度がいいのか、その答えを教えてくれるのは物理なのです。

遠投ができるとかっこいいよね 
サッカーなど他の球技でも、ボールを遠くに飛ばしたいことは多い
だから、この45度の話は、物理を学んだことのあるものなら、一度は聞いたことがある話でしょう。高校物理では「斜方投射」として勉強します。
大人ならば、「45度」が導ける?
さて、大人の皆さん、この「45度が飛距離最大」という結果を導けるだろうか。かく言う僕も、実はちゃんと計算したことがなかった気がします。無事に導き出せたので、今ひと安心しながらこの記事を書いているわけなのです。
運動方程式から出発してみましょう。
- 運動方程式から加速度・速度・距離の関係式を導いてみる
- 式を使って、問題設定を表現してみる
- 飛距離を角度で表してみる
- 飛距離の最大値を導く
早速やっていきましょう。
運動方程式から加速度・速度・距離の関係式を導いてみる

高校でも習う加速度・速度・距離の関係式は、運動方程式を積分することで得られます。
式を使って、問題設定を表現してみる
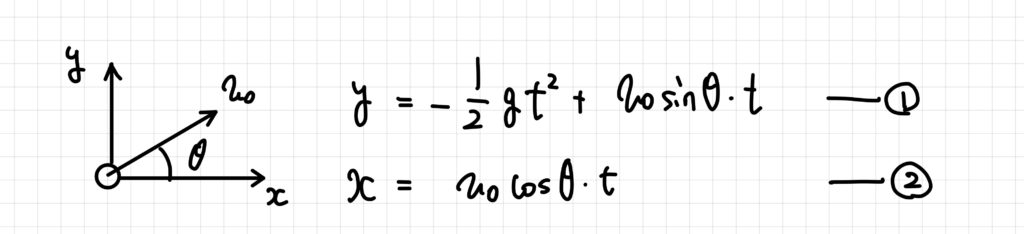
飛距離を角度で表してみる


飛距離の最大値を導く

解いてみて初めて気づいたのですが、この問題は意外と数学を使います。高校3年生で習うであろう極値の求め方や合成関数の微分の仕方を知っている必要がありますね。
しかし、ちゃんと解いていけば、無事に飛距離の最大値が算出でてきました。ちょうど高校入試で問われると、基本的な物理と数学の能力を測れる良い問題になりそうです。
角度と飛距離の関係を見てみると、こんな感じです。45度で最大値をとることは、このグラフからも確認できます。
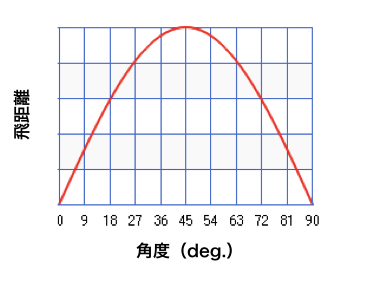
実際は45度にならない
この計算では、空気抵抗やボールの回転を無視していることに注意が必要です。
野球でも外野手がバックホームするときに投げる際には、30度くらいが良いとされています。そもそもノーバウンドで届く必要がないためです。
描画してみた
グラフを描画するには、飛距離(x)と高さ(y)の関係を単純にしておいたほうが良いでしょう。
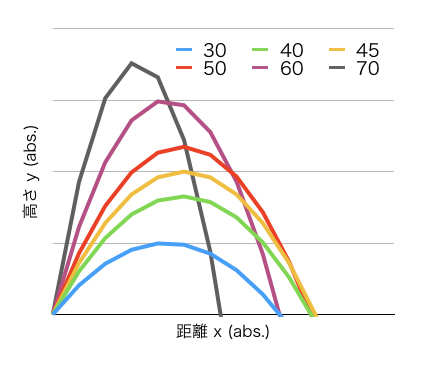
ふむふむ、わかりやすいですね。表計算ソフトで書いたので、ちょっとカクカクしているのはお許しください。
最後に
物理のなかでも力学は実感できる現象があったり、生活の役にたったりするものが多くて楽しいですよね。








